Posted by mr. rian in
Termodinamika (
bahasa Yunani:
thermos = 'panas' and
dynamic = 'perubahan') adalah
fisika energi ,
panas,
kerja,
entropi dan kespontanan proses. Termodinamika berhubungan dekat dengan
mekanika statistik di mana banyak hubungan termodinamika berasal.
Pada sistem di mana terjadi proses perubahan wujud atau pertukaran energi, termodinamika klasik tidak berhubungan dengan
kinetika reaksi (kecepatan suatu proses reaksi berlangsung). Karena alasan ini, penggunaan istilah "termodinamika" biasanya merujuk pada termodinamika setimbang. Dengan hubungan ini, konsep utama dalam termodinamika adalah
proses kuasistatik, yang diidealkan, proses "super pelan". Proses termodinamika bergantung-waktu dipelajari dalam
termodinamika tak-setimbang.
Karena termodinamika tidak berhubungan dengan konsep
waktu, telah diusulkan bahwa termodinamika setimbang seharusnya dinamakan termostatik.
Hukum termodinamika kebenarannya sangat umum, dan hukum-hukum ini tidak bergantung kepada rincian dari interaksi atau sistem yang diteliti. Ini berarti mereka dapat diterapkan ke sistem di mana seseorang tidak tahu apa pun kecual perimbangan transfer energi dan wujud di antara mereka dan lingkungan. Contohnya termasuk perkiraan Einstein tentang
emisi spontan dalam
abad ke-20 dan riset sekarang ini tentang
termodinamika benda hitam.
Konsep dasar dalam termodinamika
Pengabstrakan dasar atas termodinamika adalah pembagian dunia menjadi sistem dibatasi oleh kenyataan atau ideal dari batasan. Sistem yang tidak termasuk dalam pertimbangan digolongkan sebagai lingkungan. Dan pembagian sistem menjadi subsistem masih mungkin terjadi, atau membentuk beberapa sistem menjadi sistem yang lebih besar. Biasanya sistem dapat diberikan keadaan yang dirinci dengan jelas yang dapat diuraikan menjadi beberapa parameter !
[sunting] Sistem termodinamika
Sistem termodinamika adalah bagian dari
jagat raya yang diperhitungkan. Sebuah batasan yang nyata atau imajinasi memisahkan sistem dengan jagat raya, yang disebut lingkungan. Klasifikasi sistem termodinamika berdasarkan pada sifat batas sistem-lingkungan dan perpindahan materi, kalor dan entropi antara sistem dan lingkungan.
Ada tiga jenis sistem berdasarkan jenis pertukaran yang terjadi antara sistem dan lingkungan:
- sistem terisolasi: tak terjadi pertukaran panas, benda atau kerja dengan lingkungan. Contoh dari sistem terisolasi adalah wadah terisolasi, seperti tabung gas terisolasi.
- sistem tertutup: terjadi pertukaran energi (panas dan kerja) tetapi tidak terjadi pertukaran benda dengan lingkungan. Rumah hijau adalah contoh dari sistem tertutup di mana terjadi pertukaran panas tetapi tidak terjadi pertukaran kerja dengan lingkungan. Apakah suatu sistem terjadi pertukaran panas, kerja atau keduanya biasanya dipertimbangkan sebagai sifat pembatasnya:
- pembatas adiabatik: tidak memperbolehkan pertukaran panas.
- pembatas rigid: tidak memperbolehkan pertukaran kerja.
- sistem terbuka: terjadi pertukaran energi (panas dan kerja) dan benda dengan lingkungannya. Sebuah pembatas memperbolehkan pertukaran benda disebut permeabel. Samudra merupakan contoh dari sistem terbuka.
Dalam kenyataan, sebuah sistem tidak dapat terisolasi sepenuhnya dari lingkungan, karena pasti ada terjadi sedikit pencampuran, meskipun hanya penerimaan sedikit penarikan
gravitasi. Dalam analisis sistem terisolasi, energi yang masuk ke sistem sama dengan energi yang keluar dari sistem.
[sunting] Keadaan termodinamika
Ketika sistem dalam keadaan seimbang dalam kondisi yang ditentukan, ini disebut dalam keadaan pasti (atau keadaan sistem).
Untuk keadaan termodinamika tertentu, banyak sifat dari sistem dispesifikasikan. Properti yang tidak tergantung dengan jalur di mana sistem itu membentuk keadaan tersebut, disebut fungsi keadaan dari sistem. Bagian selanjutnya dalam seksi ini hanya mempertimbangkan properti, yang merupakan fungsi keadaan.
Jumlah properti minimal yang harus dispesifikasikan untuk menjelaskan keadaan dari sistem tertentu ditentukan oleh
Hukum fase Gibbs. Biasanya seseorang berhadapan dengan properti sistem yang lebih besar, dari jumlah minimal tersebut.
Pengembangan hubungan antara properti dari keadaan yang berlainan dimungkinkan.
Persamaan keadaan adalah contoh dari hubungan tersebut.
[sunting] Hukum-hukum Dasar Termodinamika
Terdapat empat Hukum Dasar yang berlaku di dalam sistem termodinamika, yaitu:
- Hukum Awal (Zeroth Law) Termodinamika
-
- Hukum ini menyatakan bahwa dua sistem dalam keadaan setimbang dengan sistem ketiga, maka ketiganya dalam saling setimbang satu dengan lainnya.
- Hukum Pertama Termodinamika
-
- Hukum ini terkait dengan kekekalan energi. Hukum ini menyatakan perubahan energi dalam dari suatu sistem termodinamika tertutup sama dengan total dari jumlah energi kalor yang disuplai ke dalam sistem dan kerja yang dilakukan terhadap sistem.
- Hukum kedua Termodinamika
-
- Hukum kedua termodinamika terkait dengan entropi. Hukum ini menyatakan bahwa total entropi dari suatu sistem termodinamika terisolasi cenderung untuk meningkat seiring dengan meningkatnya waktu, mendekati nilai maksimumnya.
- Hukum ketiga Termodinamika
-
- Hukum ketiga termodinamika terkait dengan temperatur nol absolut. Hukum ini menyatakan bahwa pada saat suatu sistem mencapai temperatur nol absolut, semua proses akan berhenti dan entropi sistem akan mendekati nilai minimum. Hukum ini juga menyatakan bahwa entropi benda berstruktur kristal sempurna pada temperatur nol absolut bernilai nol.
-



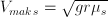



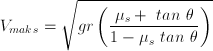
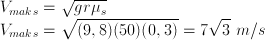













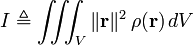

 adalah jari-jari yang digunakan untuk menentukan momen inersia
adalah jari-jari yang digunakan untuk menentukan momen inersia